Color space issues 🟠

Note

This used to be a subsection of chapter Loading from file, back when the default surface texture format was BGRA8UnormSrgb.

What is discussed here still applies whenever your target format ends with Srgb, but I moved this in an appendix because per WebGPU standard the preferred format may not only be a sRGB format. Only RGBA8Unorm or BGRA8Unorm may be returned as preferred format.

Color issue

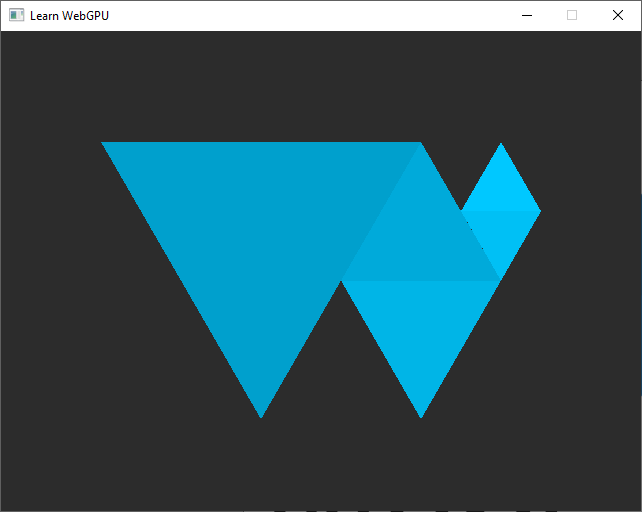
The WebGPU Logo loaded from the file, with wrong colors.

You are not just being picky, there is indeed something wrong with the colors! Compare to the logo in the left panel, the colors in the window seem lighter, and even have a different tint.

Note

This behavior depends on your device, so you may actually see correct colors. I recommend you read the following anyways though!

🙄 Hum maybe you made a mistake when writing the file you provided.

Nice try, but nope. To convince you let’s take a look at the color of the first 3 lines of the file, which correspond to the biggest triangle:

0.0 0.353 0.612

These are red, green and blue values expressed in the range \((0,1)\) but let’s remap them to the integer range \([0,255]\) (8-bit per channel) which is what your screen most likely displays (and hence what usual image file format store):

0 90 156

Now we can check on a screen capture the color of the big triangle:

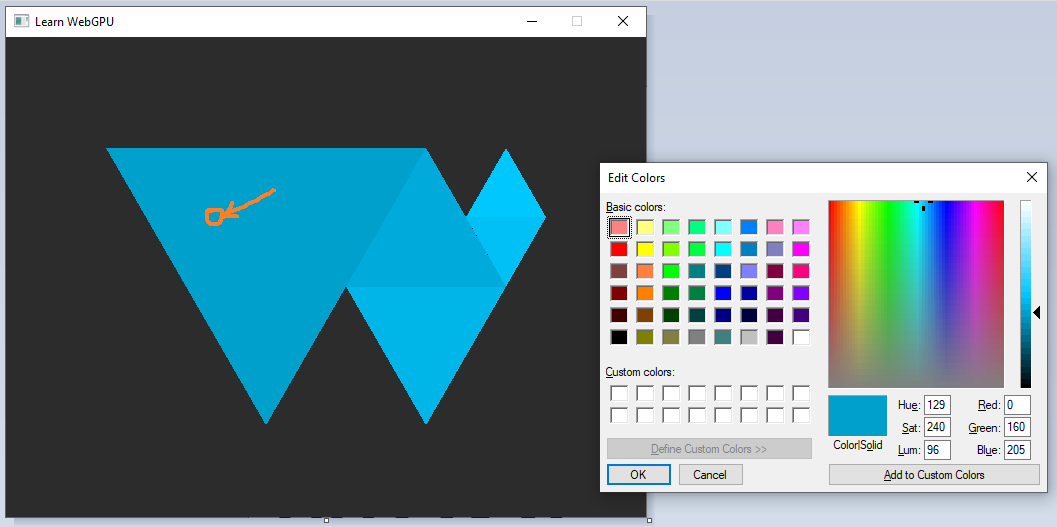
Color picking the big triangle in a screenshot of our windows shows a color of \((0, 160, 205)\).

Oh oh, it does not match. What is happening? We have a color space issue, meaning that we are expressing colors in a given space, but they end up being interpreted differently. This may happen in a lot of contexts, so it is quite useful to be aware of the basics (although color science is a non-trivial matter in general).

Our problem here comes from the surfaceFormat. Let us print it:

std::cout << "Surface format: " << surfaceFormat << std::endl;

This gives Surface format: 24. The “24” must be compared to the values of the WGPUTextureFormat enum in webgpu.h. Be aware that values there are expressed in base 16 (number literals start with 0x), so we are looking for 24 = 1 * 16 + 8 = 0x18.

Note

To avoid the need to manually handle enum values, I recommend to have a look at magic_enum. After you copy this file to your source tree you can simply do the following:

#include "magic_enum.hpp"

// [...]

std::cout << "Surface format: " << magic_enum::enum_name<WGPUTextureFormat>(surfaceFormat) << std::endl;

Thanks to advanced C++ template mechanism, this library is able to output Surface format: WGPUTextureFormat_BGRA8UnormSrgb!

Dawn

Since the Dawn implementation only supports the format BGRA8Unorm for the surface, you should directly see correct colors in that case.

In my setup, the preferred format is BGRA8UnormSrgb:

• The BGRA part means that colors are encoded with the blue channel first, then the green one, then red and alpha.

• The 8 means that each channel is encoded using 8 bits (256 possible values).

• The Unorm part means that it is exposed as an unsigned normalized value, so we manipulate floats (well, fixed-point reals actually, not floating-point) in the range \((0,1)\) even if the underlying representation only uses 8-bits. Snorm would be in range \((-1,1)\), Uint in integer range \([0,255]\), etc.

• And finally, the Srgb part tells that values use the sRGB scale.

The sRGB color space

The idea of a color space is to answer the following problem: We have a budget of 256 possible values to represent a color channel, how should these 256 discrete values (index \(i\)) be distributed along the continuous range of light intensity \(x\)?

The most intuitive approach, the linear one, consists in regularly distributing the 256 indices across the range of intensities. But we may need more precision in some parts of the range and less in others. Also, the physical response of your screen is typically not linear! Even your eyes don’t have a linear response when translating physical stimuli into psychological perception (and it depends on the surrounding lighting).

Note

The sRGB color space has been designed specifically to address the non-linearity of the display. On CRT displays, this was in line with the spontaneous response behavior of the physical device. Now we have switched to LCD or OLED display so the physical device has a different behavior, but screen manufacturer artificially reproduce the CRT response curve to ensure backward compatibility.

Important

The sRGB color space is so much of a standard that it is the one used by all common image file formats, like PNG and JPG. As a consequence, when not doing any color conversion, everything we do, including the color picking tool, is in sRGB.

However, WebGPU assumes that the colors output by the fragment shader are linear, so when setting the surface format to BGRA8UnormSrgb it performs a linear to sRGB conversion. This is what causes our colors to be wrong!

Gamma correction

An easy-fix is to force a non-sRGB texture format:

TextureFormat surfaceFormat = TextureFormat::BGRA8Unorm;

But ignoring the preferred format of the target surface may result in performance issues (the driver would need to convert formats all the time). Instead, we will handle the color space conversion in the fragment shader. A good approximation of the rRGB conversion is \(R_{\text{linear}} = R_{\text{sRGB}}^{2.2}\):

// We apply a gamma-correction to the color
// We need to convert our input sRGB color into linear before the target
// surface converts it back to sRGB.
let linear_color = pow(in.color, vec3f(2.2));
return vec4f(linear_color, 1.0);

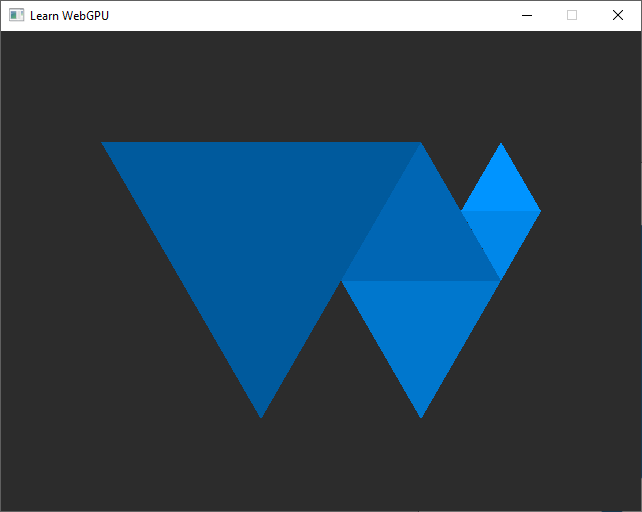
The WebGPU Logo with gamma-corrected colors.

Perfect! We fixed the problem, and we can even check with the color picker:

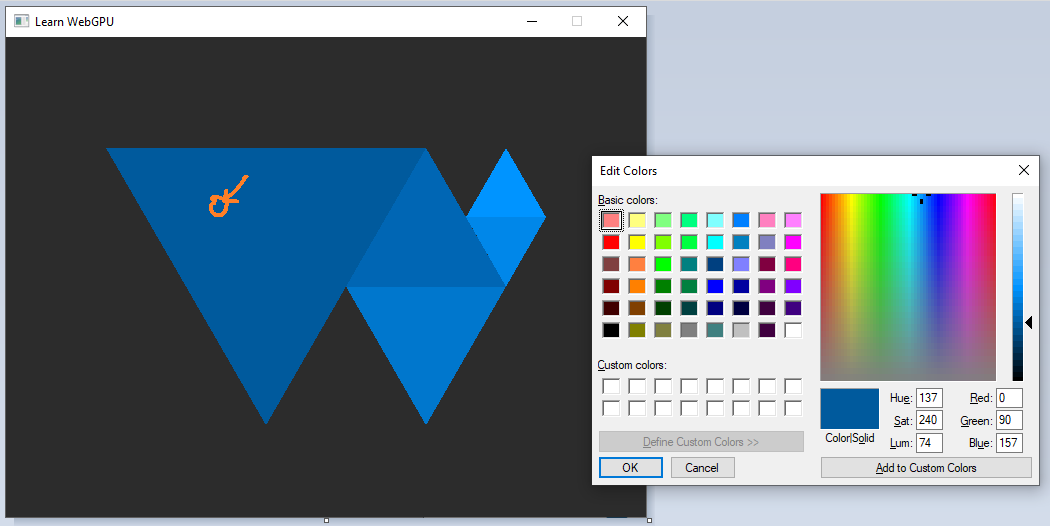
Now color picking shows the right value (almost, our gamma curve is an approximation).

This conversion from linear to non-linear color scale (or the other way around) is called gamma correction or tone mapping. Here it was for rather technical consideration, but it is common to add an artistically driven tone mapping operation at the end of a 3D rendering pipeline. And the fragment shader is the right place to do so.

Note

In general a color space is characterized by a gamut and a gamma. The gamma is this non-linearity of the discrete scale of values, and the gamut is the range of intensities that we want to cover (the vertical axis above, generalized to 3 colors). The gamut is often given by 3 primaries.

Tip

There is more generally a lot to get lost about with color spaces, don’t try to learn it all at once but I personally find it fascinating!